Distance formula - Part II

Continuing from my last post, where I told you that the distance between two points can be determined by finding the length of the hypotenuse of the right angle triangle formed from the two points.

We already know that to find the length of the hypotenuse, we apply the Theorem of Pythagoras, which says that c^2 = a^2 + b^2. (The square of the hypotenuse is equal to the sum of the squares of the remaining two sides). So from this, then, we see that we need to determine the lengths of the two sides that we have created by extending lines through our points to join at a right angle. And to find these lengths, all we need to know are the coordinates of our ! 2 points!

For a general triangle, then, we have something like this:

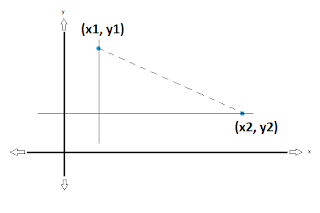
To find the horizontal length, it is just the difference between the two x-coordinates (ie. x2-x1). Think of it as taking a stick that is x2 units long, and chopping off a length of that stick that is x1 units long. The stick that you are left with, x2-x1, is the length of our horizontal side.

The same reasoning applies to find the vertical length, which is the difference between the two y-coordinates (ie. y2-y1). One comment I will make here, is that since we are talking ab! out a length of a side, the length has to be the absolute diff! erence b etween the two points (ie. you can't have a negative side length).

So then, for our general triangle, we have our 2 lengths, and let's call the hypotenuse "d" (as in, the distance between the two points).

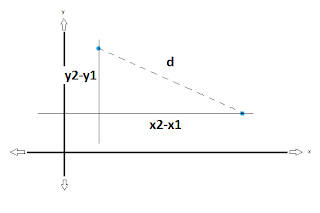
So then, if we apply the Theorem of Pythagoras to this triangle we have created, we can come up with the distance formula very easily!

c^2 = a^2 + b^2...... which we can change to read:

d^2 = (x2-x1)^2 + (y2-y1)^2

And so we have:

d = sqrt [(x2-x1)^2 + (y2-y1)^2]

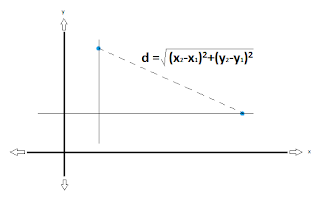
Let's quickly try with 2 points. You can draw the triangle out as I have above to follow along more closely. I will just do the quick calculation for you though.

Find the distance between the points (1,2) and (3,5).

d = sqrt [(3-1)^2 + (5-2)^2]

d = sqrt [(2)^2 + (3)^2]

d = sqrt [4 + 9]

d = sqrt [13]

And that's all there is to it. I hope that I've been able to clearly explain how to derive the distance formula. Once you know where a lot of these formulas come from, you'll never have to worry about memorizing them again! :)

solve help math