hw: ws 11.1
zero factor property calculator
Tuesday, August 31, 2010
Retirement Calculator Evaluation - Vanguard
Overall, I thought the Vanguard Retirement Calculator was a reasonably accurate estimator for how much is needed. It takes salary growth (due to inflation), social security payments, and life expectancy during retirement into account.However, if one is more than 10 years from retirement, you may need to make an adjustment to one’s estimated salary. The calculator does not account for the possibility that your salary may grow faster than inflation during your early working years – e.g. due to promotions or job changes. For those that are 10 or more years from retirement, it may be necessary to project what your! future salary may be and put the present value in the salary column. (For specifics on this economic-speak, see example #2 below.)
This calculator asks for the following information:
1. Household Income
2. Percentage of Income Needed after Retirement
3. Social Security Benefts
4. Annual Pension Benefits
5. Current Savings
6. Annual Retirement Savings Contribution
7. Annual Investment Returns
8. Years Until Retirement
9. Years in Retirement
After filling out the information, the calculator lets one know whether you have sufficient savings or the amount that one needs to save before retirement.
Example 1 – Will B. Retired is a 64 year old that will retire next year. Here is his information.
1. $50,000 total income
2. 100% income needed in retirement
3. $25,560 Social Security (used 55 year old numbers)
4. $20,000 annual pension
5. $1! 0,000 savings
6. $5,000 savings per year
7. 8% savin! gs retur n in retirement
8. 1 year until retirement
9. Life expectancy – 95, i.e. 30 years in retirement
Income needed for retirement. $52,000 in year 1. The calculator shows that Will’s retirement income will be $48,786. Most of it is covered by Social Security and his pension. This situation is acceptable since Will is so close to retirement. However, the calculator recommends Will needs to save about $185,000 more to account for the possibility of higher inflation. Thus, Will savings is currently short and should work longer before retiring.
Example 2 – Em. S. Grad is 35 years old and plans to retire at 65. Em’s information is different that Wills in #3 (social security payments), #4 (assume there are no longer pensions), and #8 (30 instead of 1 year to retirement). In addition, Em expects to retire as a Division Manager, which has a current salary of $150,000.
1. $50,000 total income
2.! 100% income needed in retirement
3. $28,638 Social Security
4. $0 annual pension
5. $10,000 savings
6. $5,000 savings per year
7. 8% savings return in retirement
8. 30 year until retirement
9. Life expectancy – 95, i.e. 30 years in retirement
Amount needed for retirement: $1,266,596 to enable $162,000 per year of retirement income. And the calculator judges that Em is on track to provide $152,036 per year, assuming Social Security payments increase at the rate of inflation. Thus, Em will need to save about $1250 more per year to reach his goal.
However, the calculator doesn’t account for non-inflation related salary increase. Thus, $1,266,596 should be Em’s minimum retirement savings target.
To account for a higher salary due to promotion or job change, I recommend that Em should use the present salary of the position he expects have in the future. For example, if Em expe! cts to be a division manager when he retires, he should input ! the $150 ,000 salary of a division manager today. (For reference, I also changed the Social Security payment to the maximum of $36,864.) With this adjustment, here is what Em would need for a retirement nest egg: $6,708,059. This would represent the high side retirement savings target. For reference, this number is close to the T.Rowe Price calculator estimate of $7,427,816, which did not include Social Security payments.
Disclaimer: Examples are illustrative purposes only. Your results will vary with different inputs and assumptions. As with all retirement calculators, please consult with your financial advisor before taking any actions.
Photo Credit: morgueFile.com, Emily Roesly
5 number summary online calculator
Fair Tax Calculator written in FLEX!
Check out the new calculator that shows how your personal wealth situation would change under the Fair Tax. While there are probably a few over zealous assumptions in there, for me it becomes obvious why I will only support Fair Tax candidates for president or congress. If you think some of their assumptions are incorrect, you can tweak them with your own figures in the last view stack/tab.
Have fun: http://www.fairtax.org/site/PageServer?pagename=calculator
zero factor property calculator
Have fun: http://www.fairtax.org/site/PageServer?pagename=calculator
zero factor property calculator
Solve Your Maths Problem with Tutor Vista
Often the case the parents have difficulty in guiding their children at home, especially if the child has difficulty doing math, especially if your child was in K-12. Your child needs help to understand math and algebra concepts, as you know that 90% is to be understood, while the remaining 10% to be memorized. This tutorial now has developed online, allowing your child can follow this tutorial from home via the internet.
In addition, if your child has difficulty with their homework, Tutor vista can also help your child to solve his homework online by using homework help menu. In this tutorial, there are also menus to solve the problems of mathematics, algebra, and trigonometry. Their tutors are always ready and willing to help you anytime on! line 24 hours a day and seven days a week. Tutor vista also provides tutoring for all math problems such as, equation, fractions, simplify and solving equations.
If you still doubt of their service, Tutor Vista also provide demo for free where you can try their services So, What are you waiting for? Just join Tutor Vista and see the result for yourself.
tutorvista demo
Trouble with Math? Get some online Math Tutoring.
TutorVista is the leading online tutoring company in the world. They offer an incredible unlimited monthly tutoring package for only $99.99 a month for all subjects - students can use their service as much as they want, whenever they nee! d it. Tutoring is available 24/7. They provide free demo for first time users where they can try the service for free.
TutorVista's online Math Help is designed to help you get the desired edge in acing the subject.
Get help in understanding algebra, calculus, precalculus, geometry, trigonometry, statistics, probability, linear programming, discrete mathematics across K-12 with their online Math tutoring program. Whether you need Math help or some quick assistance in solving Math problems before a test or an exam, their online Math tutors can help. Their tutors provide you with instant help, homework help and help with assignments in Math.
Math Help at a very affordable price
The advantage with the! ir Online Math help is that you can connect with a tutor using your PC and get personalized attention and one-on-one tutoring at a fraction of what a learning center will cost you. Also you don't waste time in travel since you study online with an online Math tutor.
Get Online Math Tutoring from the best Online Math tutor
They have online Math tutors who are experts in the subject across K-12 and beyond. ! Whatever your requirements are, the rigor and discipline of th! e TutorV ista tutor certification program will ensure that you get all that you want and more in your Math tutor. Their tutors are familiar with the National and various State Standards required across grades in the US.
Stydying Math Online is fun with TutorVista
With TutorVista's online Math tutoring and Math Homework help, studying the subject becomes easy and fun for students. Under the e! xpert guidance of our tutors, students excel in all Math related problems.
TutorVista's Online Math Tutoring gets you ahead
With TutorVista's online Math tutoring, students understand Math concepts and learn to solve Math problems quickly and easily. TutorVista sessions are just like having a tutor besides you at hom! e or in a classroom. The tutor and student talk to each other ! using vo ice (VoIP) and share an interactive whiteboard to work problems, simulations, assessments and other tasks. The one on one interactive session with the tutor helps you get an edge in the subject.
Free Online Math Help
TutorVista also offers a free demo service. Using their demo service you get free online Math help and experience the benefits of our tutoring yourself.
Come join their online Math tutor! ing program today and experience the unique TutorVista Advantage!
Learn Math with TutorVista - Get online Math tutoring, homework help anytime, anywhere.
tutorvista demo session
Stock Chart Pattern - Cranes Software (An Update)
The stock chart pattern of Cranes Software brings to mind a few stock market cliches:
1. Never try to catch a falling knife - you are supposed to wait for the knife to hit the table first, where it is likely to vibrate for a while; then it is safer to catch it. Question is: do you want to? (In the case of Cranes Software, some one seems to have removed the table which was covering a bottomless hole!)
2. Just because a stock is trading cheap, doesn't mean it can't trade cheaper.
3. Never average down in price; average up instead, because you don't know how low it can go.
The bar chart pattern of the Cranes Software stock from Mar '09 till date shows that ambition and the pursuit of growth needs to be tempered with financial prudence and patience - otherwise it may lead to annihilation:-
When I wrote about the stock back in July '09, it had made a double-bottom - 35 in Mar '09 and 34 in Jul '09 - and tried to move up. The resistance from the 50 day EMA proved too strong and the stock moved down again to 33.5 in Aug '09.
An up move on good volumes took the stock above the 50 day EMA, but a double-top at 48 proved to be its last hurrah. The stock dropped below the 50 day EMA in Oct '09 and has stayed below it till date.
A long-term support-resistance line has been drawn at 33. That level supported the stock's fall four times (marked by up arrows). This provides a cla! ssic example about support-resistance levels - which act more ! like a t hin membrane than a spring. Each test of the support (or resistance) weakens it.
After three or four tests, the support (or resistance) tends to break. Thereafter, the support usually turns into a resistance, and a resistance turns into a support. Note that after the convincing break below the support of 33 in Dec '09, the level provided resistance in Jan '10 (marked by the down arrow), and then the bottom fell out of the stock.
The MACD has remained negative since Oct '09. The RSI and slow stochastic have once again entered oversold zones.
For those who did not read my earlier analysis in July '09, the concluding paragraph is quoted below:
"The stock chart pattern of Cranes Software is a reminder of what can happen if the pursuit of growth by acquisition leads to too much debt. Even good cash flows from operations may not be enough to survive. This is not for the faint-of-heart. Intrepid investors should maintain strict stop loss at! Rs 33."
Technical analysis is not perfect. But if you don't know the basics, it can hurt you where it hurts the most in the stock market. Your wallet!
Bottomline? The stock chart pattern of Cranes Software shows that its glory days during the previous bull market are long gone, and now it is just a struggle for survival. If you own the stock, get out now. If you think it can't go lower, think again. It is game, set and match for the bears.
(Question for readers: what do you think the volume action may indicate?)
Related Post
About Support and Resistance levels in stock chart patterns
times table chart up to 100
Distance formula - Part II
Continuing from my last post, where I told you that the distance between two points can be determined by finding the length of the hypotenuse of the right angle triangle formed from the two points.
solve help math
We already know that to find the length of the hypotenuse, we apply the Theorem of Pythagoras, which says that c^2 = a^2 + b^2. (The square of the hypotenuse is equal to the sum of the squares of the remaining two sides). So from this, then, we see that we need to determine the lengths of the two sides that we have created by extending lines through our points to join at a right angle. And to find these lengths, all we need to know are the coordinates of our ! 2 points!
For a general triangle, then, we have something like this:
To find the horizontal length, it is just the difference between the two x-coordinates (ie. x2-x1). Think of it as taking a stick that is x2 units long, and chopping off a length of that stick that is x1 units long. The stick that you are left with, x2-x1, is the length of our horizontal side.
The same reasoning applies to find the vertical length, which is the difference between the two y-coordinates (ie. y2-y1). One comment I will make here, is that since we are talking ab! out a length of a side, the length has to be the absolute diff! erence b etween the two points (ie. you can't have a negative side length).
So then, for our general triangle, we have our 2 lengths, and let's call the hypotenuse "d" (as in, the distance between the two points).
So then, if we apply the Theorem of Pythagoras to this triangle we have created, we can come up with the distance formula very easily!
c^2 = a^2 + b^2...... which we can change to read:
d^2 = (x2-x1)^2 + (y2-y1)^2
And so we have:
d = sqrt [(x2-x1)^2 + (y2-y1)^2]
Let's quickly try with 2 points. You can draw the triangle out as I have above to follow along more closely. I will just do the quick calculation for you though.
Find the distance between the points (1,2) and (3,5).
d = sqrt [(3-1)^2 + (5-2)^2]
d = sqrt [(2)^2 + (3)^2]
d = sqrt [4 + 9]
d = sqrt [13]
And that's all there is to it. I hope that I've been able to clearly explain how to derive the distance formula. Once you know where a lot of these formulas come from, you'll never have to worry about memorizing them again! :)
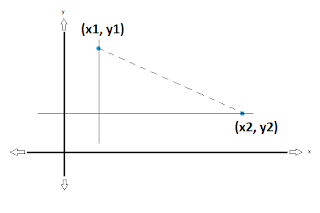
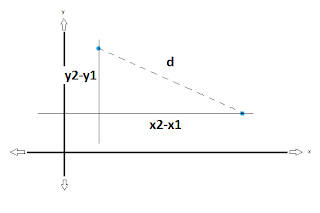
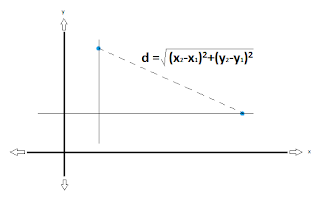
solve help math
Oliver Crisp's Attempt to Defend Penal Substitution
There have been a few attempts by contemporary philosophical theologians to explain how the Penal Substitutionary Theory (PST) of the atonement works: John Hare, Steven Porter (see here, here, and here), and Oliver Crisp. I have dealt with Hare's explanation in a previous post and I have a paper on Steven Porter's theory which I have submitted for publication in an academic journal. In this post I would like to examine Oliver Crisp's attempt to defend the PST.
In Chapter 19 of The Oxford Handbook of Philosophical Theology (eds. Thomas Flint and Michael Rea [2009], pp. 430-51), Crisp has an article entitled: "Original Sin and Atonement."
He begins the article by admitting that to this point, no one has really been able to explain how the atonement of Christ works:
The atonement is one of the central and defining doctrines of Christian theology. Yet the nature of the atonement--how it is that Christ's life and death on the cross actually atone for human sin--remains a theological conundrum (p. 430).
He continues:
In the theological literature, the relation between Christ's penal substitution for the sinner and the sinner's sin and/or guilt is usually (though not always) made sense according to what I shall call a "forensic fiction." God treats Christ as if he is guilty of the sin of fallen human beings, and "punishes" him accordingly . . . on this forensic fiction account of penal substitution, the innocent Christ really is treated as if he were the guilty sinner, though he is not. And God really does punish the innocent in the place of the guilty (p. 436).
He admits that this appears to be unjust. He states:
[W]e find no examples of legislation allowing substitution when the crime is a serious felony, such as murder. In such cases, the one guilty must meet the penal consequences of that crime, and we would consider it a terrible miscarriage of justice were a substitute punished in place of the perpetrator (p. 436).
What the defender of the theological application of penal substitution needs is some reason for thinking that it is just for God to punish Christ in place of the sinner. . . For, whatever else the defender of penal substitution says, unlike pecuniary penal substitution, it certainly looks unjust that Christ, an innocent individual, should be punished in place of me, a sinful individual (p. 437)
This injustice Crisp attempts to solve through what he terms: Realist Penal Substitution. He draws the term from the Realist theory of the imputation of sin which goes back to Augustine. Augustine taught that in a real sense every human being was present in Adam when he sinned. He phrased it this way: In the first man, therefore, there existed the whole human nature, which was to be transmitted by the woman to posterity, when that conjugal union received the divine sentence of its own condemnation; and what man was made, not when created, but when he sinned and was punished, this he propagated, so far as the origin of sin and death are concerned(City of God, 13:3). According to Augustine, we were all present seminally in Adam. Building on this, Crisp states:
We begin with the idea that Adam and his progeny are (somehow) one metaphysical entity such that God may justly pass on the moral consequences of Adam's sin to his heirs because they are all member of one persisting entity, or object, that we might call "Fallen Humanity" (p. 438).
Now applying this realism doctrine to the atonement, Crisp writes:
Consider the possibility that Christ and the elect together compose one metaphysical entity that persists through time, just as, on the Augustinian realist way of thinking, Adam and his progeny do. This object we shall dub "Redeemed Humanity". Christ is in some sense the first member of this entity, and the elect are subsequent members (p. 440).
Because Christ is part of this "metaphysical entity," which Crisp calls "Redeemed Humanity," he shares the guilt (or penal consequences) of the elect's sin (even though he himself is sinless) and thus can justly die for that guilt. Crisp explains:
Although he is not the one who has sinned, or the part of the mass of Redeemed Humanity that has sinned, because he is a member of this larger entity, he may pay the consequences of the sin of other members of the same entity, by which I mean the derivatively elect, like you and me (p. 441).He maintains that this solution does not involve imputation and thus escapes the charge of being a "legal fiction."
Notice that there is no "imputation" involved in this process, no forensic fiction, whereby God treats Christ as if he were the sinner for the purpose of bringing about atonement, as with many traditional accounts of penal substitution. The transference of the punishment for sin from fallen humanity to Christ, and the union of those self-same humans with Christ are two aspects of Christ's atoning work that involve a real union between Christ and the human beings concerned (pp. 441-42).
He believes that his proposed Realist Penal Substitution Theory avoids
the moral problems besetting other, standard arguments for penal substitution that require only that Christ acts on behalf of sinful humans as their representative ... [which] requires a forensic fiction in order to make good on the act of atonement. It is this that has generated so much of the difficulties facing apologists for penal substitution. This problem is not so much overcome as circumvented by the realist accounts of penal substitution offered here, because Christ's act of atonement is not merely representationalist; he really takes upon himself the penal consequences for human sin. (p. 443)
What are some of the problems with Crisp's Realist Penal Subsitution Theory?
1. Whereas one can imagine how that every human being could be seminally in Adam (assuming he was literally the first man) and thereby have an organic (and genetic) connection with him, the same does not hold true for the "metaphysical entity" which Crisp calls, "Redeemed Humanity." There is no real connection between the parts. At best it is some type of mystical unity which defies any meaningful description.
2. If there were some real connection between the parts in Crisp's metaphysical Redeemed Humanity entity, then it seems that Jesus would share not only in the guilt (and penal consequences) of the other members but in the actual corruption and demerit of the sins of the other members. How can he share in one but not in the other? Moreover, guilt and its penal consequences only have meaning when attached to the sin itself. In other words, a person is only guilty and subject to punishment for a particular sin that he commits. You cannot decouple sin and guilt.
3. It seems at best what Crisp's "solution" does is to make Jesus guilty by association. In other words, since Jesus is the head of the metaphysical entity and since other members of the entity are sinners and subject to the penal consequences of that sin, then Jesus is also guilty and subject to the same consequences by means of his association with them. This "guilt by association" is generally recognized as a fallacy. In reality, what Crisp is arguing for is what I have previously termed "collective culpability." While the concept of collective culpability was prevalent in ancient times, it is generally rejected today (e.g., a major philosophical discussion took place after WW II in which the question was raised: "Are the German people as a whole culpable for what the Nazi's did?" The consensus of scholars was "No." See Collective Responsibility: Five Decades of Debate in Theoretical and Applied Ethics, eds. Larry May and Stacey Hoffman [1992]).
Allow me to offer an illustration. A new CEO takes over for BP. He has no personal responsibility for the oil spill in the gulf as he was not associated with the company at the time of the spill. However, now as the CEO, he is the head of the corporation which is culpable for the spill. Thus, if the whole corporation is punished, he will be punished as well (even though he personally is innocent). That makes sense because he voluntarily attached himself to the corporation knowing that it was going to be subject to punishment (another example would be a football coach who takes over a program that is about to enter NCAA probation). However, to single out the CEO and make him pay personally in place of the corporation would make no sense. It seems that in the PST, this is what is happening when Jesus bears the punishment that the whole entity deserves.
solve by substitution
Car Pooling - Energy Conservaton Project
My commitment to student teaching this year has put a damper on my extra spending money. I have been pondering the question, "how can I save money when I'm not really making money?" Frustrating. As I considered how I spend my money, I realized that my car was one of the biggest expenses. Given that gas is at sky high prices, and I only live five miles from school, it made sense for me to start carpooling. My fiance, Scott, who conveniently drives by Houston Middle School on his way to work everyday will be my mode of transportation for a week.Questions:
* How much money will I save by car pooling for a week???
* How much money will I save by car pooling in my car versus Scott's truck???
Assumption:
* I think that I will save $20.00 a week by car pooling to work
Require! ments for my Research:
* I will also need to figure out how many miles per gallon Scott's truck gets.
* I will drive to school to and from school for one week.
* I will then car pool with Scott to and from school for one week.
* During this two week period of time I will keep a record of my data and my results that I find.
promethium board
A regular expression to check for prime numbers
Today i came across this article regarding regular expression to check for prime numbers.
It is really wonderful and i thank Avinash for putting in his blog.
Below code is used in java to achieve the same.
import java.util.regex.Pattern;
Few Notes:
if we keenly see what exactly this expression
It matches with "1″ followed by one or more ones minimally. This means that it matches with "11″ initially.
The string obtained initially is bound to the variable
\1+ then matches with whatever has been matched above ("11″ initially) repeated one or more times! .
Let’s try to apply it to 9.
"1″ * 9 = "111111111″. (11+?) matches "11″ initially. \\1+ cannot match because there are 7 remaining ones. Backtracking occurs. (11+?) now matches "111″. And here \\1+ matches the remaining 6 remaining ones! Hence, 9 is not prime.
Cool isn't it?
Source: http://www.noulakaz.net/weblog/2007/03/18/a-regular-expression-to-check-for-prime-numbers/
prime expression
It is really wonderful and i thank Avinash for putting in his blog.
Below code is used in java to achieve the same.
import java.util.regex.Pattern;
public class ArtlTest {
public static void main(String[] args) {
int! c =7;
String s = "";
while (c > 0) {
c--;
s+="1";
}
System.out.println(!Pattern.matches("^1?|^(11+?)\\1+", s));
}
}
Few Notes:
if we keenly see what exactly this expression
(11+?)\\1+)is doing
It matches with "1″ followed by one or more ones minimally. This means that it matches with "11″ initially.
The string obtained initially is bound to the variable
\\1.
\1+ then matches with whatever has been matched above ("11″ initially) repeated one or more times! .
Let’s try to apply it to 9.
"1″ * 9 = "111111111″. (11+?) matches "11″ initially. \\1+ cannot match because there are 7 remaining ones. Backtracking occurs. (11+?) now matches "111″. And here \\1+ matches the remaining 6 remaining ones! Hence, 9 is not prime.
Cool isn't it?
Source: http://www.noulakaz.net/weblog/2007/03/18/a-regular-expression-to-check-for-prime-numbers/
prime expression
Precalculus help
Introduction to study free calculus helps:- Study Free Calculus Helps Example Problems
precalculus help
Study free calculus helps involves the process of learning problems in calculus from free websites and also find calculus help free. Calculus is one of the parts of mathematics which deals with finding rate of the change of the given function with respect to change in the input function. Calculus is separated into differential calculus and integral calculus to find the rate of change. The following are the example problems in calculus to study with the helps of free websites.
Study Free Calculus Helps Example Problems
and also math homework solver is here to help you:
Example 1:
Simplify the non linear function by differentiation.
f(s) = 2s 3 – 5s 6 + 7s
Solution:
The given function is
f(s) = 2s 3 – 5s 6 + 7s
Perform differentiation operation for the given function the solution to all your Math! problem
! f '(s) = 2(3 s 2) – 5(6s 5 ) + 7
Solving the above terms we get,
f '(s) = 6s 2 – 30s 5 + 7 is the answer.
precalculus help
So Long ...
And so we begin where we left off ... don't let the sky be your limit. ;-)
I'm so glad we've had this time together,
Just to have a laugh or learn some math,
Seems we've just got started and before you know it,
Comes the time we have to say, "So Long!"
So long everybody! Watch this space for pointers to new blogs for each of my classes.
Farewell, Auf Wiedersehen, Adieu, and all those good bye things. ;-)
precalculus
March, my birthday, and I'm still here!
Hi Readers! I am still here responding to people's requests for homework help, I just don't post the answers on my blog as much anymore. But rest assured, I am still here answering your emails.
Also, to celebrate my birthday this week, I invite you to partake in this fun online gaming experience called "Auditorium"!
http://www.playauditorium.com/
I enjoyed it so much that I played it all the way through on my first sitting!
math homework help for free
The Oregon Carbon Calculator
My carbon footprint.
Rudy Berg of the SW Oregon chapter of the Northwest Eco-Building Guild regularly keeps many of us here in Eugene informed of events, articles, or links of interest on the subject of living and designing sustainably. One of his recent e-mail blasts introduced me to the Oregon Carbon Calculator.
The Oregon Carbon Calculator is a new interactive tool on the DEQ website that lets Oregon residents measure their carbon footprint and discover ways to improve it. The tool calculates all direct and indirect greenhouse gas emissions from personal transportation, household energy use, and consumption of food, goods and services.
It’s fun and easy to use. You’ll find out how your household's carbon footprint compares to households of similar size and income here in Oregon. You’ll also learn how you can take action to reduce your carbon footprint from a number of specific ideas and strategies.
I calculated that the total carbon footprint for me and my wife is 75% of comparable households in the state. Good for us. However, it’s still 380% of the global average. The per person resource demand in this country is about 8.5 hectares versus the world average of about 2.2 hectares. We’re running an ecological deficit, with a footprint larger than our biological capacity.
There are numerous other online tools (such as Carbon Footprint) for assessing the size of one’s carbon footprint but I had not previously sought them out. Thanks, Rudy, for informing me about the Oregon Carbon Calculator.
The Oregon Carbon Calculator is made possible through Oregon DEQ's support of the CoolClimate Network, a program of the University of California, Berkeley, and through financial support by the California Air Resources Board and the CoolCalifornia.org partnership. Oregon DEQ selected this calculator for its approach and depth in calculating human impacts to climate change.
how many hours until calculator
Cereal Box Generator.
Upload an image from your computer. (Width must be less then 150 pixels. Height needs to be less than 250 pixels. Upload only images that end in: .jpg) When you're satisified with your work, you can print out your box. To create the box, you'll just need to cut away the grey area and fold in the tabs.
(thanks Ruth)
[ Cereal Box Generator ]
box plot generator
(thanks Ruth)
[ Cereal Box Generator ]
box plot generator
Online Algebra Tutor
Internet has changed the way we learn and communicate. Want to learn more about a topic? Just do some searches or take help from specialized sites on that particular topic. Want to continue your study, but don't have time to attend classes? Just enroll for an online course and get your degree from the comfort of your own home.
Similarly, want to help your kids complete their homework assignments on time? Just contact a good online tutoring service and the rest will be taken care of by the online tutors. It will give you complete peace of mind. How? Imagine a situation where your child needs some help with Algebra and you are unable to ! find any good tutor. What you gonna do? Continue your search or simply get an online tutor. Your Online algebra tutor will not only help your child with their homework or assignments, but will also help your child understand major concepts of Algebra.
Nowadays, there are many online tutoring services that promises to take care of your child's study. But all are not same. Some may provide excellent service, while some may just want to take your money. So, take care while choosing an online tutor for your kids. Consult with others and go with the most reliable one.
Looking for a reliable online tutoring service? Let's return to your case. Want Algebra help for your child? Try TutorVista, an education services company that provide online tutoring to needful for K-12 and college students around the world. Their service covers many subjects and tutoring! is done in an one-on-one secure web environment by using the ! latest t echnologies. So, all you need to have is a computer with a broadband connection. Their unique virtual whiteboard works much like a traditional blackboard, where both student and tutor can write to share problems and answers. Even your child can chat with the Algebra tutor by using their instant messaging service.
What about the charges? Their monthly unlimited online tutoring package will cost you $99.99. In my view, this is a reasonable price. Because, TutorVista's online tutoring service is available 24-hours a day, 7 days a week and there is no limit for maximum number of tutoring sessions. You can connect to the tutor, whenever and wherever your child needs help. If you want, you can also try their free demo.
So, get an online algebra tutor today and see your child excel in school. I am sure that you won't regret!
Similarly, want to help your kids complete their homework assignments on time? Just contact a good online tutoring service and the rest will be taken care of by the online tutors. It will give you complete peace of mind. How? Imagine a situation where your child needs some help with Algebra and you are unable to ! find any good tutor. What you gonna do? Continue your search or simply get an online tutor. Your Online algebra tutor will not only help your child with their homework or assignments, but will also help your child understand major concepts of Algebra.
Nowadays, there are many online tutoring services that promises to take care of your child's study. But all are not same. Some may provide excellent service, while some may just want to take your money. So, take care while choosing an online tutor for your kids. Consult with others and go with the most reliable one.
Looking for a reliable online tutoring service? Let's return to your case. Want Algebra help for your child? Try TutorVista, an education services company that provide online tutoring to needful for K-12 and college students around the world. Their service covers many subjects and tutoring! is done in an one-on-one secure web environment by using the ! latest t echnologies. So, all you need to have is a computer with a broadband connection. Their unique virtual whiteboard works much like a traditional blackboard, where both student and tutor can write to share problems and answers. Even your child can chat with the Algebra tutor by using their instant messaging service.
What about the charges? Their monthly unlimited online tutoring package will cost you $99.99. In my view, this is a reasonable price. Because, TutorVista's online tutoring service is available 24-hours a day, 7 days a week and there is no limit for maximum number of tutoring sessions. You can connect to the tutor, whenever and wherever your child needs help. If you want, you can also try their free demo.
So, get an online algebra tutor today and see your child excel in school. I am sure that you won't regret!
algebra tutoring online
Printable TAKS Tests Math Reading, Science, Social Studies All Grades
All years, all grades, both English and Spanish, with answer keys.
Solving two step equations activities
Gauss: Construction of regular polygons
It was not enough for Carl Friedrich Gauss to prove the constructibility a heptadecagon (a seventeen sided polygon). He generalized the idea to come up with the theorem that I will present today.
The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.
Lemma 1: The periods of two terms are (2 cos 2kπ/p) for k = 1 ... (p-1)/2
Proof:
(1) ηj = ζj + ζ[j + (p-1)/2] [See Definition 3, here where e = (p-1)/2 and f = 2]
(2) ζ[j + (p-1)/2] = (ζj)g(p-1)/2 [See Definition 1, here]
(3) g(p-1)/2 ≡ -1 (mod p) since:
(a) (g(p-1)/2)2 ≡ gp-1 (mod p)
(b) gp-1 ≡ 1 (mod p) [By Fermat's Little Theorem, see here]
(c) Thus, g(p-1)/2 ≡ ± 1 (mod p)
(d) But since g is a primitive root modulo p (see D! efinition 2 and Definition 4, here) and since (p-1)/2 is less than p-1, it follows that g(p-1)/2 ≠ 1.
(e) Thus, we have that g(p-1)/2 ≡ -1 (mod p).
(4) So, we have ηj = ζj + ζj-1 [See Lemma 1, here]
(5) We can expre! ss the p-th roots of unity as solutions to Φp(x) such that they are the solution to:
xp-1 + xp-2 + ... + 1 = 0 [See Lemma 1, here]
(6) The trigonometric solution for the equation above are (see Corollary 1.1, here):
cos 2kÏ€/p + isin 2kÏ€/p where 1 ≤ k ≤ p-1.
(7) For ζj, there exists an integer m such that:
ζj = cos 2mπ/p + i sin 2mπ/p
(8) Using Lemma 4, here, where u= 2mπ/p, we have:
ζj + ζj-1 = cos 2mπ/p + i sin 2mπ/p + cos 2mπ/p - isin 2mπ/p = 2 cos 2m π/p.
QED
Theorem 2: If p is a prime number of the form p = 2m+1 (with m ∈ N) then the regular polygon with p sides can be constructed with ruler and compass.
Proof:
(1) Since p=2m + 1, p-1 is a power of 2.
(2) We can thus view p-1 as a chain of multiplications such as:
1 → 2 → ... → 2m-2 → 2m-1 → 2m
(3) Using a previous result (see Lemma 5, here), we can see that the chain of multiplication in step #2 shows that the periods of two terms can be determined by solving a sequence of quadratic equations.
(4) The periods of two terms are the values 2 cos 2kπ/p for k = 1 ... (p-1)/2 [See Lemma 1 above]
(5) Since the solution of a quadratic equation only requires rational operations and extraction of square roots (see Theorem, here), it follows that cos 2Ï€/p can be obtained from 0 and 1 by rational operations and extractions of roots.
(6) So, using Wantzel's Constructibility Criterion (see Theorem 5, here), it follows that (cos 2Ï€/p, 0) is constructible.
(7) Let A be a point at (0,a) and O at (0,0) such that we take OA as one unit of measurement and circleOA is a unit circle (see here for details if needed on unit circles)
(8) Point P0 = (cos 2Ï€/p, sin 2Ï€/p) is obtained in the following way:
(a) Let Q be the point at (cos 2Ï€/p, 0) that we showed was constructible in step #6 above.
(b) Let QP0 be a line that is perpendicular to OQ and where P0 intersects with the unit circle OA. [See here for Euclid, Book I, Proposition 11 whic! h shows this construction]
(c) Now, we can see that P0 is at (cos 2Ï€/p, sin 2Ï€/p) since:
By the diagram above:
x = cos 2Ï€/p
r = 1
Since cos θ = (cos 2π/p)/1 = cos 2π/p, we have θ = 2π/p.
Also, we have: sin θ = sin 2π/p = y/1 ! = y
(9) The point P0 is a vertex of the regular polygon with p sides. The line AP0 forms one side of the polygon, so we can label point A as P1.
(10) We can find the other p-1 sides in the following way. Let P0P1 be a circle at point P1 with radius equal to P0P1 (see Postulate 2, here). Call P2 the point where circle P0P1 intersects with unit circle OA (and is not point P0). We can repeat for circle P2P1 (finding point P3), circle P3P2 (find point P4), etc. until we have constructed our regular p-sided figure.
QED
Corollary 2.1: A regular polygon with n sides can be constructed with a ruler and compass if n is a product of distinct Fermat primes and a power of 2.
Proof:
(1) A regular polygon with n sides is constructible when n is a Fermat prime. [By Theorem 2 above]
(2) Since we can always do a repeated bisection of angles (see here for Euclid's Elements, Book I, Prop 9), a regular polygon with n sides is also constr! uctible when n is a po! wer of < span style="font-weight: bold;">2.
(3) So, to complete this proof, we only need to show that if n1 and n2 are relatively prime and a polygon with n1 sides is constructible and a polygon with n2 sides is constructible, then it follows that a polygon with n1n2 sides is constructible.
(4) Since n1, n2 are relatively prime, there exists! integers m1, m2 such that (see Lemma 1, here):
m1n1 + m2n2 = 1.
(5) Multiplying both sides by 2Ï€/(n1n2) gets us:
m1(2Ï€/n< /span>2) + m2(2Ï€/n1) = 2Ï€/(n1n2)
(6) Therefore using Wantzel's Criterion (see Theorem 5, here), it follows that 2Ï€/(n1n2) can be constructed by repeating a certain number of times 2Ï€/n1 and 2Ï€/n2.
(7) It therefore follows that the regular polygon with n1n2 sides can be constructed from regular n1 polygon and a regular n2 polygon.
QED
References
regular polygon angles
The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.
Lemma 1: The periods of two terms are (2 cos 2kπ/p) for k = 1 ... (p-1)/2
Proof:
(1) ηj = ζj + ζ[j + (p-1)/2] [See Definition 3, here where e = (p-1)/2 and f = 2]
(2) ζ[j + (p-1)/2] = (ζj)g(p-1)/2 [See Definition 1, here]
(3) g(p-1)/2
(a) (g(p-1)/2)2 ≡ gp-1 (mod p)
(b) gp-1 ≡ 1 (mod p) [By Fermat's Little Theorem, see here]
(c) Thus, g(p-1)/2 ≡ ± 1 (mod p)
(d) But since g is a primitive root modulo p (see D! efinition 2 and Definition 4, here) and since (p-1)/2 is less than p-1, it follows that g(p-1)/2 ≠ 1.
(e) Thus, we have that g(p-1)/2 ≡ -1 (mod p).
(4) So, we have ηj = ζj + ζj-1 [See Lemma 1, here]
(5) We can expre! ss the p-th roots of unity as solutions to Φp(x) such that they are the solution to:
xp-1 + xp-2 + ... + 1 = 0 [See Lemma 1, here]
(6) The trigonometric solution for the equation above are (see Corollary 1.1, here):
cos 2kÏ€/p + isin 2kÏ€/p where 1 ≤ k ≤ p-1.
(7) For ζj, there exists an integer m such that:
ζj = cos 2mπ/p + i sin 2mπ/p
(8) Using Lemma 4, here, where u= 2mπ/p, we have:
ζj + ζj-1 = cos 2mπ/p + i sin 2mπ/p + cos 2mπ/p - isin 2mπ/p = 2 cos 2m π/p.
QED
Theorem 2: If p is a prime number of the form p = 2m+1 (with m ∈ N) then the regular polygon with p sides can be constructed with ruler and compass.
Proof:
(1) Since p=2m + 1, p-1 is a power of 2.
(2) We can thus view p-1 as a chain of multiplications such as:
1 → 2 → ... → 2m-2 → 2m-1 → 2m
(3) Using a previous result (see Lemma 5, here), we can see that the chain of multiplication in step #2 shows that the periods of two terms can be determined by solving a sequence of quadratic equations.
(4) The periods of two terms are the values 2 cos 2kπ/p for k = 1 ... (p-1)/2 [See Lemma 1 above]
(5) Since the solution of a quadratic equation only requires rational operations and extraction of square roots (see Theorem, here), it follows that cos 2Ï€/p can be obtained from 0 and 1 by rational operations and extractions of roots.
(6) So, using Wantzel's Constructibility Criterion (see Theorem 5, here), it follows that (cos 2Ï€/p, 0) is constructible.
(7) Let A be a point at (0,a) and O at (0,0) such that we take OA as one unit of measurement and circle
(8) Point P0 = (cos 2Ï€/p, sin 2Ï€/p) is obtained in the following way:
(a) Let Q be the point at (cos 2Ï€/p, 0) that we showed was constructible in step #6 above.
(b) Let QP0 be a line that is perpendicular to OQ and where P0 intersects with the unit circle OA. [See here for Euclid, Book I, Proposition 11 whic! h shows this construction]
(c) Now, we can see that P0 is at (cos 2Ï€/p, sin 2Ï€/p) since:
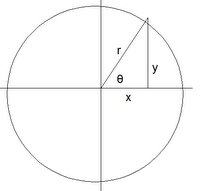
By the diagram above:
x = cos 2Ï€/p
r = 1
Since cos θ = (cos 2π/p)/1 = cos 2π/p, we have θ = 2π/p.
Also, we have: sin θ = sin 2π/p = y/1 ! = y
(9) The point P0 is a vertex of the regular polygon with p sides. The line AP0 forms one side of the polygon, so we can label point A as P1.
(10) We can find the other p-1 sides in the following way. Let P0P1 be a circle at point P1 with radius equal to P0P1 (see Postulate 2, here). Call P2 the point where circle P0P1 intersects with unit circle OA (and is not point P0). We can repeat for circle P2P1 (finding point P3), circle P3P2 (find point P4), etc. until we have constructed our regular p-sided figure.
QED
Corollary 2.1: A regular polygon with n sides can be constructed with a ruler and compass if n is a product of distinct Fermat primes and a power of 2.
Proof:
(1) A regular polygon with n sides is constructible when n is a Fermat prime. [By Theorem 2 above]
(2) Since we can always do a repeated bisection of angles (see here for Euclid's Elements, Book I, Prop 9), a regular polygon with n sides is also constr! uctible when n is a po! wer of < span style="font-weight: bold;">2.
(3) So, to complete this proof, we only need to show that if n1 and n2 are relatively prime and a polygon with n1 sides is constructible and a polygon with n2 sides is constructible, then it follows that a polygon with n1n2 sides is constructible.
(4) Since n1, n2 are relatively prime, there exists! integers m1, m2 such that (see Lemma 1, here):
m1n1 + m2n2 = 1.
(5) Multiplying both sides by 2Ï€/(n1n2) gets us:
m1(2Ï€/n< /span>2) + m2(2Ï€/n1) = 2Ï€/(n1n2)
(6) Therefore using Wantzel's Criterion (see Theorem 5, here), it follows that 2Ï€/(n1n2) can be constructed by repeating a certain number of times 2Ï€/n1 and 2Ï€/n2.
(7) It therefore follows that the regular polygon with n1n2 sides can be constructed from regular n1 polygon and a regular n2 polygon.
QED
References
- Jean-Pierre Tignol, Galois' Theory of Algebra! ic Equations
, World Scientific, 2001
regular polygon angles
Differences between Determinants and Matrices
Determinants and matrices, they look alike. Their similarities caught many unaware and results in "excitements" and much interests.
Both contain numbers within. But ......
- determinants are bounded by two straights lines whereas matrices are by square braces
- determinant resulted in a single numerical value, whereas matrices are sets of numbers grouped within the braces
- determinant can be extracted from matrix, but not the other way round
- there are inverse matrix but not inverse determinant
- a scalar multiplier affects only a single row or single column of a determinant, but affects all the numbers within a matrix
The differences are aplenty. But those listed above are the least any maths students or person should know.
Why create such topics to excite maths learners?
Answer: So that maths will be made interesting and challenging (... the informal reply)
With open m! indedness, maths is a very fantastic subject to learn and train for. It carries many hard works and beautiful thinking. Thoughts that are simple yet abstract at times.
Any more fun? ..... You are the answer!
.
determinants of matrices
Both contain numbers within. But ......
- determinants are bounded by two straights lines whereas matrices are by square braces
- determinant resulted in a single numerical value, whereas matrices are sets of numbers grouped within the braces
- determinant can be extracted from matrix, but not the other way round
- there are inverse matrix but not inverse determinant
- a scalar multiplier affects only a single row or single column of a determinant, but affects all the numbers within a matrix
The differences are aplenty. But those listed above are the least any maths students or person should know.
Why create such topics to excite maths learners?
Answer: So that maths will be made interesting and challenging (... the informal reply)
With open m! indedness, maths is a very fantastic subject to learn and train for. It carries many hard works and beautiful thinking. Thoughts that are simple yet abstract at times.
Any more fun? ..... You are the answer!
.
determinants of matrices
LOVE AFFAIRS and DIFFERENTIAL EQUATIONS
From Albert Einstein's notebooks, on a sweet spring day in the early days of The Institute for Advanced Study at Fine Hall in Princeton once upon a time, on his attempt to solve The Three-body Problem:*
Modeling of Love-Hate relationships (from here)
See: Strogatz S.H., Love Affairs and differential equations, Math. Magazine, 61,35,1988.
Lets imagine a Romeo (R) and Juliet (J) "troubled" romance, where:
R(t)=Romeo's Love/Hate for Juliet at time t
J(t)= Juliet's Love/Hate for Romeo at time t
with positive values signifying love and negative values hate.
A first order system of equations to model the evolution in time of the relationship can be written as (Rdot = dR/dt = rate of change of R, and similarly for Jdot):
Rdot = a R + b J
Jdot = c R + d J
where a,b,c,d are parameters which can be positive, negative or zero, with the following "meanings":
a and d: "cautiousness" (throw towards (if a,d>0) the other or avoid (if a,d<0) the other)
b and c: "responsiveness" (degree at which they react to the other's advances)
For instance a case where Romeo has both a>0 and b>0 can be called an "eager beaver" (he gets excited by Juliet's love and is further excited by his own feelings into a "snowball of affection").
But if a<0 and b>0 ("cautious lover"), it means that the more Romeo loves Juliet (R>0), the more he wants to "run away" from her (Rdot more negative, particularly acute near marriage decisions...); and the more he hates her (R<0) the more he increases his love (Rdot more positive, nothing like distance to inflame his fellings).
If a<0 and b<0 ("cautious and unresponsive") usually not a good chance for romance, "lets just be friends" type...
If a>0 and b<0 ("daring but unresponsive") is more the "narcisist" type...
Typical issues of these "dynamical love systems" is which relationships are "viable"...
Notice that the "fixed points", that is where the system will stabilize would be given by
Rdot=0
Jdot=0
that is :
a R + b J =0
c R + d J =0
which is a system of two algebraic equations with two unknowns (R and J).
Let's analyze some special cases:
1) Two identical cautious lovers: a=d<0 , b=c>0
Then det=ad-bc=a2 -b2 , and the solutions behave in the following way:
i) If a2>b2 the lovers are more cautious than "responsive" and the relationship "fizzles out " to mutual indifference R=J=0 (caution leads to apathy)
ii) If a2
2) Out of touch with their own feelings: a=0, d=0 (lovers only react to the others feelings)
Then det=ad-bc=-bc, and the equations are:
Rdot = b J
Jdot = c R
Find out what happens!
3) Do opposites attract? Analyze d=-a, c=-b.
4) Do identical lovers make for good couples? d=a, c=b
5) Analyze your own "made up" case of interest!
Here's what interests me, the Eurorock band "T'Pau" performing their 1987 hit, "Heart and Soul":
second order differential equations
* - OK, I lied, sorry. That is NOT from Einstein's notebooks. I don't know where it's from, but it's funny. :-)
No need to explore three bodies for the moment though. The two body problem is easier, is linear, and here's a sweet application by Strogatz:
First, click here to see a New York Times guest columnist piece by Stephen Strogatz on Romeo-and-Juliet Mathematics. The replies are pretty funny. :-)
Click here to see Strogatz' original 1988 piece on the topic.
See: Strogatz S.H., Love Affairs and differential equations, Math. Magazine, 61,35,1988.
Lets imagine a Romeo (R) and Juliet (J) "troubled" romance, where:
R(t)=Romeo's Love/Hate for Juliet at time t
J(t)= Juliet's Love/Hate for Romeo at time t
with positive values signifying love and negative values hate.
A first order system of equations to model the evolution in time of the relationship can be written as (Rdot = dR/dt = rate of change of R, and similarly for Jdot):
Rdot = a R + b J
Jdot = c R + d J
where a,b,c,d are parameters which can be positive, negative or zero, with the following "meanings":
a and d: "cautiousness" (throw towards (if a,d>0) the other or avoid (if a,d<0) the other)
b and c: "responsiveness" (degree at which they react to the other's advances)
For instance a case where Romeo has both a>0 and b>0 can be called an "eager beaver" (he gets excited by Juliet's love and is further excited by his own feelings into a "snowball of affection").
But if a<0 and b>0 ("cautious lover"), it means that the more Romeo loves Juliet (R>0), the more he wants to "run away" from her (Rdot more negative, particularly acute near marriage decisions...); and the more he hates her (R<0) the more he increases his love (Rdot more positive, nothing like distance to inflame his fellings).
If a<0 and b<0 ("cautious and unresponsive") usually not a good chance for romance, "lets just be friends" type...
If a>0 and b<0 ("daring but unresponsive") is more the "narcisist" type...
Typical issues of these "dynamical love systems" is which relationships are "viable"...
Notice that the "fixed points", that is where the system will stabilize would be given by
Rdot=0
Jdot=0
that is :
a R + b J =0
c R + d J =0
which is a system of two algebraic equations with two unknowns (R and J).
Let's analyze some special cases:
1) Two identical cautious lovers: a=d<0 , b=c>0
Then det=ad-bc=a2 -b2 , and the solutions behave in the following way:
i) If a2>b2 the lovers are more cautious than "responsive" and the relationship "fizzles out " to mutual indifference R=J=0 (caution leads to apathy)
ii) If a2
2) Out of touch with their own feelings: a=0, d=0 (lovers only react to the others feelings)
Then det=ad-bc=-bc, and the equations are:
Rdot = b J
Jdot = c R
Find out what happens!
3) Do opposites attract? Analyze d=-a, c=-b.
4) Do identical lovers make for good couples? d=a, c=b
5) Analyze your own "made up" case of interest!
Here's what interests me, the Eurorock band "T'Pau" performing their 1987 hit, "Heart and Soul":
second order differential equations
Adding and Subtracting Fractions
Working with fractions is one of the most difficult concepts for students. This week I am going to go through some interactives and web tools that will help students add and subtract fractions with both common denominators and without common denominators. In my experience students have problems with Adding and subtracting fractions in all the levels of mathematics, from Math Foundations to AP Calculus. It seems to be a concept that students don’t grasp early on, and then struggle with throughout their math education. The following is a list of interactives and activities that can really help students work through their struggles with Adding and subtracting fractions. I believe adding a visual element to this concept will help students tremendousl! y. This list is just a few of the interactives that I have found online. Please feel free to look even further and share your findings with all of us.
This is a tutorial that goes through many concepts dealing with fractions, including Adding and subtracting fractions.
Adding and subtracting fractions Interactive
This interactive shows a visual representation of a fraction while working through addition/subtraction problems with common and unlike denominators.
This interactive allows students to create their own game depending on what skill they want to practice.
This game asks students to select the correct answer to an addition/subtraction problem while a fish scoops the correct answer up.
This game asks students to select the correct answer as they are riding in ! a boat. The answers are held up by bugs flying by the window o! f the bo at.
This is a list of fraction quizzes that students can complete to practice their skills.
I hope that this is helpful for students who are struggling with Adding and subtracting fractions. Next week we will work through multiplication and division of fractions.
Adding and subtracting fractions
Writing Process
1. Plan your writing
2. Write your draft (book)
3. Typed on computer with double spacing
4. Edit as I type
5. Once I have finished typing:
6. Print
7. This is where I really edit my work – checking to make sense, annotate,
add info/take out info, use any checklist I may have, grammar,
punctuation, spelling. Always thinking to myself 'How can I make this
better!'
8. Get someone to check
9. Before I publish I must have a conference with Mr McKay
10. Fix my writing
11. PUBLISH
2. Write your draft (book)
3. Typed on computer with double spacing
4. Edit as I type
5. Once I have finished typing:
6. Print
7. This is where I really edit my work – checking to make sense, annotate,
add info/take out info, use any checklist I may have, grammar,
punctuation, spelling. Always thinking to myself 'How can I make this
better!'
8. Get someone to check
9. Before I publish I must have a conference with Mr McKay
10. Fix my writing
11. PUBLISH
Adding fractions examples
Students Interpretations
This is a detail from a Mandala design by a dear continuing Sacred Geometry student Christianna Kreiss. Since taking her first class, Christianna continues to create lots of beautiful Mandalas, Rose windows and other designs.
Check out examples of works that the students have created over the past Sacred Geometry class sessions. I've kept their works as anonymous to respect their privacy. Enjoy!
constructions geometry
Check out examples of works that the students have created over the past Sacred Geometry class sessions. I've kept their works as anonymous to respect their privacy. Enjoy!
AA1o
constructions geometry
Distance formula - Part II
Continuing from my last post, where I told you that the distance between two points can be determined by finding the length of the hypotenuse of the right angle triangle formed from the two points.
Angle of Intersection between Curves Answers
We already know that to find the length of the hypotenuse, we apply the Theorem of Pythagoras, which says that c^2 = a^2 + b^2. (The square of the hypotenuse is equal to the sum of the squares of the remaining two sides). So from this, then, we see that we need to determine the lengths of the two sides that we have created by extending lines through our points to join at a right angle. And to find these lengths, all we need to know are the coordinates of our ! 2 points!
For a general triangle, then, we have something like this:
To find the horizontal length, it is just the difference between the two x-coordinates (ie. x2-x1). Think of it as taking a stick that is x2 units long, and chopping off a length of that stick that is x1 units long. The stick that you are left with, x2-x1, is the length of our horizontal side.
The same reasoning applies to find the vertical length, which is the difference between the two y-coordinates (ie. y2-y1). One comment I will make here, is that since we are talking ab! out a length of a side, the length has to be the absolute diff! erence b etween the two points (ie. you can't have a negative side length).
So then, for our general triangle, we have our 2 lengths, and let's call the hypotenuse "d" (as in, the distance between the two points).
So then, if we apply the Theorem of Pythagoras to this triangle we have created, we can come up with the distance formula very easily!
c^2 = a^2 + b^2...... which we can change to read:
d^2 = (x2-x1)^2 + (y2-y1)^2
And so we have:
d = sqrt [(x2-x1)^2 + (y2-y1)^2]
Let's quickly try with 2 points. You can draw the triangle out as I have above to follow along more closely. I will just do the quick calculation for you though.
Find the distance between the points (1,2) and (3,5).
d = sqrt [(3-1)^2 + (5-2)^2]
d = sqrt [(2)^2 + (3)^2]
d = sqrt [4 + 9]
d = sqrt [13]
And that's all there is to it. I hope that I've been able to clearly explain how to derive the distance formula. Once you know where a lot of these formulas come from, you'll never have to worry about memorizing them again! :)
Angle of Intersection between Curves Answers
Drawing WPF Curves with Arrow heads
Having drawn the shapes, the curves and found their intersection point, I finally needed to draw an arrow head. In order to draw the arrow at the right angle we need to know the tangent of the Bezier curve at the intersection point. Since that is beyond my maths capability I chose to find the intersection point between the line and an imaginary, slightly larger, rectangle that surrounds the target shape. The difference between the two intersection points provides the required angle for the arrow head.
private static void DrawArrowHead(Canvas canvas, PathGeometry linePath, Rect shapeRect, Color color)
{
// Get the intersection point of the imaginary, slightly
// larger rectangle that surrounds the targer shape.
Rect! outerRect = new Rect(shapeRect.Left - 10, shapeRect.Top - 10, shapeRect.Width + 20, shapeRect.Height + 20);
RectangleGeometry shapeGeometry = new RectangleGeometry(shapeRect);
Point[] intersectPoints = GetIntersectionPoints(linePath, shapeGeometry);
double innerLeft = intersectPoints[0].X;
double innerTop = intersectPoints[0].Y;
shapeGeometry = new RectangleGeometry(outerRect);
intersectPoints = GetIntersectionPoints(linePath, shapeGeometry);
double outerLeft = intersectPoints[0].X;
double outerTop = intersectPoints[0].Y;
Polygon arrowHead = new Polygon();
arrowHead.Points = new PointCollection();
arrowHead.Points.Add(new Point(innerLeft, innerTop));
arrowHead.Points.Add(new Point(innerLeft + 10, innerTop + 5));
arrowHead.Points.Add(new Point(innerLeft + 10, innerTop - 5));
arrowHead.Points.Add(new Point(inner! Left, innerTop));
arrowHead.Stroke = new SolidColorBru! sh(color );
arrowHead.Fill = new SolidColorBrush(color);
// The differences between the intersection points on
// the inner and outer shapes gives us the base and
// perpendicular of the right-angled triangle
double baseSize = innerLeft - outerLeft;
double perpSize = innerTop - outerTop;
// Calculate the angle in degrees using ATan
double angle = Math.Atan(perpSize / baseSize) * 180 / Math.PI;
// Rotate another 180 degrees for lines in the 3rd & 4th quadrants
if (baseSize >= 0) angle += 180;
// Apply the rotation to the arrow head
RotateTransform rt = new RotateTransform(angle, innerLeft, innerTop);
arrowHead.RenderTransform = rt;
// Arrow heads are drawn over the lines but
// under the shapes
Canvas.SetZIndex(arrowHead, (int)Layer.Arrow);
canvas.Children.Add(arrowHead);
}
How to do Angle of Intersection between Curves
Solve Your Maths Problem with Tutor Vista
Often the case the parents have difficulty in guiding their children at home, especially if the child has difficulty doing math, especially if your child was in K-12. Your child needs help to understand math and algebra concepts, as you know that 90% is to be understood, while the remaining 10% to be memorized. This tutorial now has developed online, allowing your child can follow this tutorial from home via the internet.
In addition, if your child has difficulty with their homework, Tutor vista can also help your child to solve his homework online by using homework help menu. In this tutorial, there are also menus to solve the problems of mathematics, algebra, and trigonometry. Their tutors are always ready and willing to help you anytime on! line 24 hours a day and seven days a week. Tutor vista also provides tutoring for all math problems such as, equation, fractions, simplify and solving equations.
If you still doubt of their service, Tutor Vista also provide demo for free where you can try their services So, What are you waiting for? Just join Tutor Vista and see the result for yourself.
trigonometry tutoring
Wall Wisher Trigonometry
Tomorrow my Year 9 maths students get introduced to Trigonometry for the first time, and so they will need an online 24x7 online web-based Help site.
Good old "Wall Wisher" to the rescue, and this time we built the whole wall in one session, and did not move any post it notes around. This resulted in no problems or glitches whatsoever, and so this approach is definitely the one to use when building walls.
Note that we had previously done all our Internet research and had all the links and items we wanted to put onto the wall in a notepad text file.
If you would like to see the wall full size, then click this link:
http://www.wallwisher.com/wall/trigonometry9
The best thing about Trig are the sine shaped sound wave graphs, and even better than this is the electronic manipulation of these sound waves by electronic sound effects pedals like these ones right here:
Just about my dream collection of Boss beauties right there for sure.
So that's about it, and now it's time for us to "sine" off :)
Enjoy,
Big Passy Wasabi
online trigonometry
Subscribe to:
Posts (Atom)